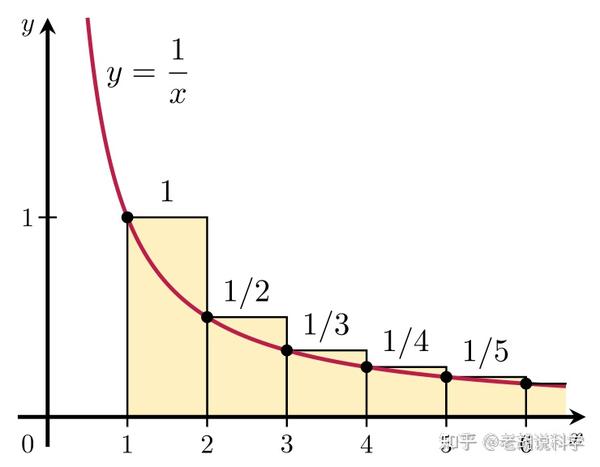
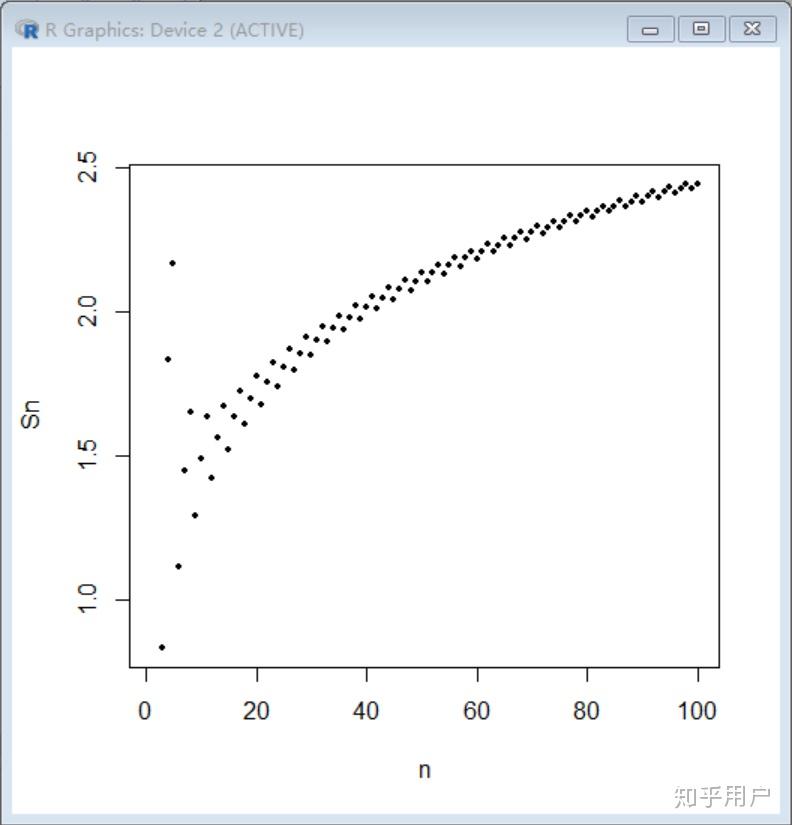
麻豆网站视频在线观看,av一区在线播放,日本在线视频不卡,国产精品一区二区a
国产精品一区二区黑丝|
国产黑丝在线一区二区三区|
国产精品久久影院|
一区二区国产盗摄色噜噜|
五月天久久比比资源色|
黄色小说综合网站|
欧洲在线/亚洲|
国产日韩精品一区|
五月天激情小说综合|
国产成人精品免费看|
欧美喷水一区二区|
国产精品婷婷午夜在线观看|
秋霞午夜av一区二区三区|
成人一区二区视频|
欧美剧情片在线观看|
国产精品美女久久久久久久
|
一区二区三区欧美视频|
激情久久五月天|
欧美激情在线一区二区三区|
午夜精品国产更新|
91一区二区在线|
久久久精品黄色|
调教+趴+乳夹+国产+精品|
91麻豆免费看片|
亚洲国产精品国自产拍av|
麻豆专区一区二区三区四区五区|
在线观看精品一区|
亚洲免费色视频|
成人黄动漫网站免费app|
久久这里只有精品视频网|
日本女人一区二区三区|
91黄色免费版|
伊人婷婷欧美激情|
色综合色综合色综合色综合色综合|
久久亚洲二区三区|
麻豆一区二区三|
精品国产乱子伦一区|
蜜臀av一级做a爰片久久|
欧美精品色综合|
偷窥国产亚洲免费视频|
欧美狂野另类xxxxoooo|
日韩精品免费专区|
欧美精品xxxxbbbb|
日本在线不卡视频一二三区|
欧美一区二区精品在线|
久久精品国产一区二区三|
精品福利一二区|
国产一区二区伦理片|
久久精品在线观看|
丁香婷婷综合色啪|
国产精品福利一区|
色先锋aa成人|
亚洲午夜精品在线|
欧美情侣在线播放|
另类欧美日韩国产在线|
久久嫩草精品久久久精品一|
国产精品18久久久久久久久久久久|
久久久亚洲国产美女国产盗摄|
国产精品一区三区|
亚洲视频网在线直播|
欧美视频在线播放|
热久久免费视频|
久久精品欧美日韩精品|
91麻豆福利精品推荐|
天天色图综合网|
26uuu久久综合|
97精品久久久午夜一区二区三区
|
heyzo一本久久综合|
亚洲欧洲日产国产综合网|
91麻豆swag|
免费观看一级欧美片|
精品少妇一区二区三区免费观看|
国产精品99久久久久|
亚洲欧美另类图片小说|
欧美精品日韩综合在线|
韩国av一区二区|
亚洲女与黑人做爰|
日韩一区二区在线观看|
日韩一区二区三区四区|
国产一区免费电影|
国产精品白丝在线|
欧美剧情片在线观看|
丁香亚洲综合激情啪啪综合|
性欧美疯狂xxxxbbbb|
久久久精品日韩欧美|
欧美亚洲国产怡红院影院|
国产在线视视频有精品|
一区二区日韩av|
久久精品一区八戒影视|
欧美影院精品一区|
高清不卡一区二区|
午夜精品在线看|
国产精品美女久久久久aⅴ|
欧美日韩国产首页在线观看|
成人免费看片app下载|
日本女优在线视频一区二区|
亚洲激情中文1区|
国产喷白浆一区二区三区|
91麻豆精品国产91|
欧美在线你懂的|
aa级大片欧美|
精品影院一区二区久久久|
亚洲一区二区av电影|
国产精品欧美精品|
日韩精品一区二|
欧美日韩综合不卡|
97久久精品人人做人人爽|
国产一二精品视频|
日韩av中文字幕一区二区三区|
亚洲视频一区在线观看|
欧美韩日一区二区三区四区|
欧美xxxxx裸体时装秀|
欧美日韩色综合|
色偷偷一区二区三区|
成人免费看片app下载|
国产精品 欧美精品|
久久不见久久见中文字幕免费|
亚洲电影第三页|
一区二区三区免费网站|
亚洲天堂网中文字|
国产一区二区三区精品视频|
日韩精品欧美精品|
午夜久久久久久久久久一区二区|
亚洲精品视频观看|
亚洲男女一区二区三区|
亚洲女人小视频在线观看|
中文字幕视频一区二区三区久|
国产精品视频一二三区|
日本一区二区三区dvd视频在线|
日韩美女在线视频|
日韩欧美一区二区三区在线|
日韩欧美精品在线|
日韩视频123|
精品国产sm最大网站免费看
|
午夜视频在线观看一区|
亚洲一级片在线观看|
亚洲国产日韩精品|
亚洲一二三区视频在线观看|
一区二区在线电影|
亚洲一区免费在线观看|
亚洲影院久久精品|
一区二区三区久久久|
亚洲国产人成综合网站|
日本美女视频一区二区|
久久激情五月婷婷|
国内精品免费在线观看|
粉嫩一区二区三区在线看|
成人综合在线观看|
99视频在线观看一区三区|
91麻豆福利精品推荐|
欧美日韩综合在线|
精品久久久久久无|
国产精品网站一区|
一区二区在线观看免费|
日韩精品免费视频人成|
国产一区日韩二区欧美三区|
成人影视亚洲图片在线|
在线中文字幕一区二区|
欧美一区二区三区免费|
国产免费观看久久|
一区二区三区在线影院|
欧美日韩亚洲综合在线|
日韩午夜激情免费电影|
久久久久久毛片|
亚洲品质自拍视频网站|
日韩黄色在线观看|
国产一区二区三区久久久|
亚洲黄色av一区|
另类中文字幕网|
91在线精品秘密一区二区|
欧美日韩久久一区|
国产亚洲成av人在线观看导航|
亚洲日本韩国一区|
日韩黄色片在线观看|
精品一区精品二区高清|
99国内精品久久|
在线播放欧美女士性生活|
精品国产乱码久久久久久影片|
亚洲天堂中文字幕|
奇米精品一区二区三区在线观看|
国内外成人在线|
在线观看亚洲成人|
久久影音资源网|
午夜欧美大尺度福利影院在线看|
国产剧情一区在线|
99热这里都是精品|
欧美电视剧在线观看完整版|
一区二区三区日韩|
懂色av一区二区夜夜嗨|
欧美一区二区网站|
中文字幕免费一区|
中文字幕一区日韩精品欧美|
日本欧美加勒比视频|
在线影视一区二区三区|
日韩精品一区二区三区swag|
亚洲第四色夜色|
成人一区二区在线观看|
精品国产乱码久久久久久蜜臀
|
99国产精品久久久|
亚洲精品在线三区|