好的，以下是根據(jù)您的要求生成的文章：

調(diào)和級數(shù)為什么發(fā)散？揭示背后的數(shù)學奧秘

你是否曾經(jīng)遇到過一個數(shù)學問題，涉及到調(diào)和級數(shù)并發(fā)現(xiàn)它似乎總是發(fā)散，而不是收斂到你預期的結(jié)果？今天我們將深入探討調(diào)和級數(shù)為什么會發(fā)散，揭示其背后的數(shù)學原理和邏輯。

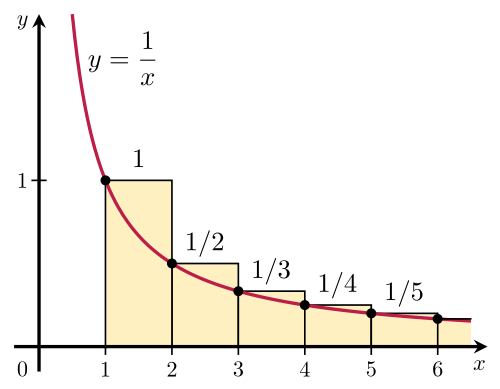
首先，我們需要了解調(diào)和級數(shù)的定義。調(diào)和級數(shù)是由一系列遞減的分數(shù)構(gòu)成的數(shù)列，其分子為常數(shù)，分母從1開始逐漸增加。當我們在計算調(diào)和級數(shù)的部分和時，這些分數(shù)的和并不會趨近于某個特定的值，而是無限制地增加。這是因為每個分數(shù)的值雖然很小，但由于數(shù)列中的項數(shù)無限多，這些小的值累積起來會導致部分和不斷增大，最終導致發(fā)散。

與調(diào)和級數(shù)形成鮮明對比的是等差數(shù)列和等比數(shù)列，這兩種數(shù)列的和在一定條件下可以收斂到有限的值。但調(diào)和級數(shù)的特性在于其分母的增長速度無法抵消分子累加造成的增長趨勢。換句話說，盡管每個分數(shù)的值越來越小，但由于分數(shù)的數(shù)量無限多，它們累積的效果足以讓調(diào)和級數(shù)發(fā)散。

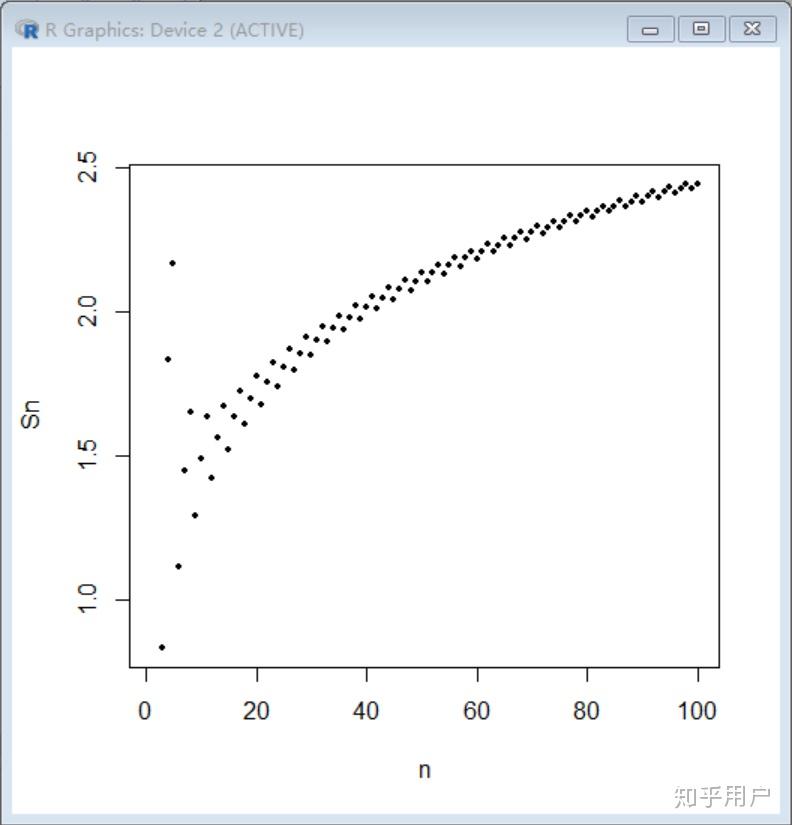
為了更直觀地理解這一點，我們可以考慮調(diào)和級數(shù)的部分和。隨著項數(shù)的增加，部分和的增長速度會越來越快，因為沒有明顯的上限來限制它的增長。這種無限制的增長正是調(diào)和級數(shù)發(fā)散的直觀表現(xiàn)。

總的來說，調(diào)和級數(shù)的發(fā)散性源于其分子不變而分母逐漸增加的特性，以及無窮多的項數(shù)導致的累積效應。這個問題不僅涉及到數(shù)學的基本原理，也是無窮級數(shù)理論中的重要課題之一。希望這篇文章能幫助你更深入地理解調(diào)和級數(shù)的奧秘。